Trigonometric Ratios In Right Triangles

The vi trigonometric ratios are sine (sin), cosine (cos), tangent (tan), cotangent (cot), cosecant (cosec), and secant (sec). In geometry, trigonometry is a branch of mathematics that deals with the sides and angles of a right-angled triangle. Therefore, trig ratios are evaluated with respect to sides and angles.

The trigonometry ratios for a specific angle 'θ' is given below:

Trigonometric Ratios
Sin θ	Reverse Side to θ/Hypotenuse
Cos θ	Adjacent Side to θ/Hypotenuse
Tan θ	Reverse Side/Adjacent Side & Sin θ/Cos θ
Cot θ	Adjacent Side/Opposite Side & 1/tan θ
Sec θ	Hypotenuse/Adjacent Side & 1/cos θ
Cosec θ	Hypotenuse/Opposite Side & 1/sin θ

Note: Opposite side is the perpendicular side and the adjacent side is the base of the right-triangle. Besides, bank check out trigonometric functions to learn about each of these ratios or functions in item.Trigonometric Identities

Definition

Trigonometric Ratios are defined as the values of all the trigonometric functions based on the value of the ratio of sides in a right-angled triangle. The ratios of sides of a right-angled triangle with respect to any of its acute angles are known equally the trigonometric ratios of that particular angle.

The three sides of the right triangle are:

Hypotenuse (the longest side)
Perpendicular (opposite side to the angle)
Base of operations (Adjacent side to the angle)

Trigonometric Identities
Trigonometric Ratios of Complementary Angles
Trigonometric Ratios Of Standard Angles
Trigonometry Angles
Trigonometry Formulas
Trigonometry Values

How to Observe Trigonometric Ratios?

Consider a right-angled triangle, right-angled at B.

Trigonometric ratios

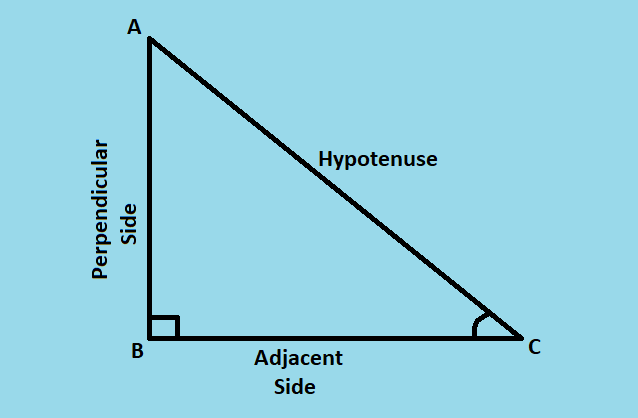
With respect to ∠C, the ratios of trigonometry are given equally:

sine: Sine of an angle is divers as the ratio of the side contrary(perpendicular side) to that angle to the hypotenuse.
cosine: Cosine of an angle is defined as the ratio of the side adjacent to that angle to the hypotenuse.
tangent: Tangent of an bending is divers every bit the ratio of the side opposite to that angle to the side adjacent to that angle.
cosecant: Cosecant is a multiplicative inverse of sine.
secant: Secant is a multiplicative inverse of cosine.
cotangent: Cotangent is the multiplicative inverse of the tangent.

The higher up ratios are abbreviated as sin, cos, tan, cosec, sec and tan respectively in the lodge they are described. So, for Δ ABC, the ratios are defined as:

sin C = (Side opposite to ∠C)/(Hypotenuse) = AB/AC

cos C= (Side adjacent to ∠C)/(Hypotenuse) = BC/Air conditioning

tan C = (Side opposite to ∠C)/(Side adjacent to ∠C) = AB/BC = sin ∠C/cos ∠C

cosec C= i/sin C = (Hypotenuse)/ (Side Opposite to ∠C)=AC/AB

sec C = 1/cos C = (Hypotenuse)/ (Side Reverse to ∠C)= AC/BC

cot C = ane/tan C = (Side adjacent to ∠C)/(Side opposite to ∠C)= BC/AB

In right Δ ABC, if ∠Aand ∠C are assumed every bit 30° and 60°, then there can exist infinite right triangles with those specifications just all the ratios written in a higher place for ∠C in all of those triangles will exist same. So, all the ratios for any of the acute angles (either ∠A or ∠C) will be the same for every correct triangle. This ways that the ratios are contained of lengths of sides of the triangle.

Trigonometric Ratios Table

The trigonometric ratios for some specific angles such as 0 °, 30 °, 45 °, 60 ° and ninety° are given below, which are unremarkably used in mathematical calculations.

Angle	0°	xxx°	45°	60°	xc°
Sin C	0	1/2	1/√ii	√3/two	1
Cos C	1	√three/ii	ane/√ii	1/ii	0
Tan C	0	1/√iii	1	√three	∞
Cot C	∞	√3	1	1/√iii	0
Sec C	1	2/√3	√2	ii	∞
Cosec C	∞	2	√two	2/√three	1

From this table, we tin find the value for the trigonometric ratios for these angles. Examples are:

Sin 30° = ½
Cos 90° = 0
Tan 45° = ane

Trigonometry Applications

Trigonometry is i of the most important branches of mathematics. Some of the applications of trigonometry are:

Measuring the heights of towers or big mountains
Determining the distance of the shore from the bounding main
Finding the distance between ii celestial bodies
Determining the power output of solar prison cell panels at different inclinations
Representing different physical quantities such as mechanical waves, electromagnetic waves, etc.

Information technology is evident from the higher up examples that trigonometry has its involvement in a major role of our twenty-four hour period-to-day life and much more than. In virtually of the applications listed above, something was being measured and that is what trigonometry is all about.

Solved Problems

Q.i: If in a right-angled triangle ABC, right-angled at B, hypotenuse Ac = 5cm, base BC = 3cm and perpendicular AB = 4cm and if ∠ACB = θ, then find tan θ, sin θ and cos θ.

Sol: Given,

In ∆ABC,

Hypotenuse, AC = 5cm

Base, BC = 3cm

Perpendicular, AB = 4cm

Then,

tan θ = Perpendicular/Base = 4/three

Sin θ = Perpendicular/Hypotenuse = AB/Air-conditioning = ⅘

Cos θ = Base/Hypotenuse = BC/AC = ⅗

Q.2: Find the value of tan θ if sin θ = 12/5 and cos θ = ⅗.

Sol: Given, sin θ = 12/5 and cos θ = ⅗

As we know,

Tan θ = Sin θ/Cos θ

Tan θ = (12/five)/(⅗)

Tan θ = 12/3

Tan θ = 4

Practice Questions

Discover the value of sin θ, if tan θ = ¾ and cos θ = ½.
Observe tan θ if sin θ = 4/3 and cos θ = 3/2
Notice sec θ, if cos θ = 9/viii
Detect cosec θ, if sin θ 16/five

Video Lesson

Trigonometric Ratios of Compound Angles

Download BYJU'S App and acquire thousands of concepts here through interesting and personalised videos.

Oftentimes Asked Questions – FAQs

What are the three master trigonometric ratios?

The three primary trigonometric ratios are tangent (tan), sine (sin) and cosine (cos).

What are the vi trigonometric ratios?

The half dozen 6 trigonometric ratios are sine, cosine, tangent, cotangent, cosecant, and secant.

What is SOH CAH TOA?

SOH CAH TOA is the mnemonic to remember the formula for trigonometry ratios, such that:
SOH: Sine part is the ratio of Opposite side and Hypotenuse
CAH: Cosine is the ratio of Next Side and Hypotenuse
TOA: Tangent is the ratio of Reverse side and Adjacent Side

What is the formula for Cotangent, Secant and Cosecant?

Cotangent is the ratio of Next side and Reverse side, (Base of operations/Perpendicular)
Secant is the ratio of hypotenuse and adjacent side, (Hypotenuse/Base)
Cosecant is the ratio of hypotenuse and opposite side (Hypotenuse/Perpendicular)

What is the human relationship between sin, cos and tan?

Tangent functions is equal to the ratio of sine and cosine function.
Tan θ = Sin θ/Cos θ