Vertical Dilation Vs Horizontal Dilation

Dr. J'southward Maths.com
Where the techniques of Maths
are explained in simple terms.

Functions - Transformations.
Summary of shift and dilation transformations.

The post-obit is a summary of the strategies outlined in the video for transformations aiming at shifting and/or dilating curves.

	Vertical		Horizontal
Shifts	Replace y with y - V.		Supersede 10 with ten - H.
	V is the constant by which the curve is moved vertically.		H is the abiding by which the curve is moved horizontally.
		V > 0: moves bend up.		H > 0: moves bend to right.
		V < 0: moves curve downward.		H < 0: moves curve to left.

Dilation	Replace y with .		Supplant y with.
	V is the dilation factor from the x centrality.		H is the dilation factor from the y axis
		V > one: curve expands up.		H > one: curve expands out.
		0 < Five < ane: curve contracts towards x axis.		0 < H < 1: bend contracts towards y axis.
		Five < 0: curve flips effectually x-axis.		H < 0: curve flips around y-axis.

The following table provides examples of transformations together with descriptions.
The f(ten) is not the aforementioned across all examples do the basic shape is provided:

Transformation	Equation	Graph
Horizontal shift:	y = x³ transformed to y = (10 + 2)³. The +two in the brackets moves the curve 2 units to the left.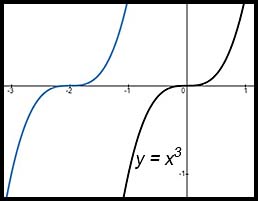
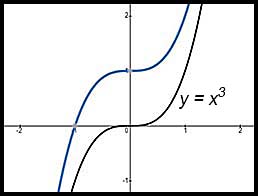Vertical shift:	y = x³ transformed to y = tenⁱⁱⁱ + 1 moves up i (note the +one is not attached to the ten term.
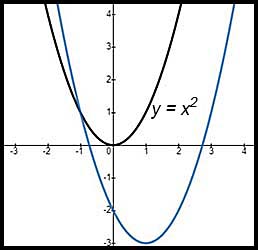Both shifts:	y = x² transformed to y = (x - ane)ⁱⁱ - three moves horizontally 1 to the correct moves vertically 3 down.
Dilation	y = f(ten) transformed to 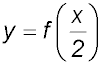. The two inside the office shows a horizontal dilation - or stretch) by a factor of 2. The betoken (-i, 0) becomes (-ii, 0).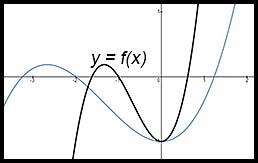
	y = f(x) transformed to y = 2f(ten) is equivalent to y ÷ two = f(ten). Hence a vertical dilation (a stretch) by a factor of 2 - e.g. the y = -1 goes to y = -2. (no change to the 10 intercepts of course).
Mixtures	y = f(ten) transformed to y = 1 - f(x): the negative in forepart of f(10) flips the curve effectually the x axis (greenish curve); the +i moves the whole curve up i unit (blueish curve).
	y = f(ten) is transformed into y = i - 2f(3x): the three coefficient for ten shrinks the width of f(ten) by a cistron of iii (so the curve is narrower) - a partitioning by 1/3; the 2 in front of the function can be idea of as existence a division by ½ and and so further shrinks the curve horizontally (reducing the 10 values);
		the negative sign flips the function effectually the x axis; the +1 moves the curve upwardly i unit of measurement.